Starting an Active Learning experiment

Each active learning experiment starts with zero labeled samples. In that case, no supervised query strategy can be used. It is common to select the first batch of samples at random however it is proposed in Diverse mini-batch Active Learning to use a clustering approach for the first batch. This example shows how to perform this.

We start with necessary imports and initializations

from matplotlib import pyplot as plt
import numpy as np
from time import time

from sklearn.datasets import load_digits
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import train_test_split
from sklearn.cluster import KMeans

from cardinal.uncertainty import MarginSampler
from cardinal.clustering import KMeansSampler
from cardinal.random import RandomSampler
from cardinal.plotting import plot_confidence_interval
from cardinal.base import BaseQuerySampler
from cardinal.zhdanov2019 import TwoStepKMeansSampler
from cardinal.utils import ActiveLearningSplitter

np.random.seed(7)

The parameters of this experiment are:

• batch_size is the number of samples that will be annotated and added to the training set at each iteration,

• n_iter is the number of iterations in the simulation.

We use the digits dataset and a RandomForestClassifier.

batch_size = 45
n_iter = 8

X, y = load_digits(return_X_y=True)
X /= 255.
n_samples = X.shape[0]

model = RandomForestClassifier()

Core Active Learning Experiment

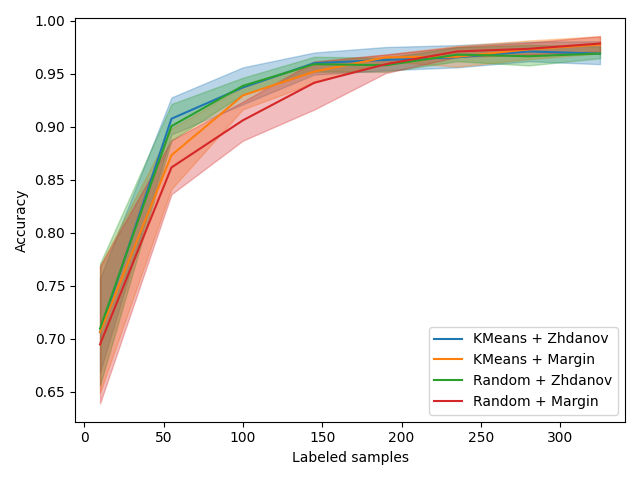
We now compare our class sampler to Zhdanov, a simpler KMeans approach and, of course, random. For each method, we measure the time spent at each iteration and we plot the accuracy depending on the size of the labeled pool but also time spent.

starting_samplers = [
    ('KMeans', KMeansSampler(batch_size)),
    ('Random', RandomSampler(batch_size)),
]

samplers = [
    ('Zhdanov', TwoStepKMeansSampler(5, model, batch_size)),
    ('Margin', MarginSampler(model, batch_size)),
]

#figure_accuracies = plt.figure().number


for starting_sampler_name, starting_sampler in starting_samplers:
    for sampler_name, sampler in samplers:

        all_accuracies = []

        for k in range(4):
            splitter = ActiveLearningSplitter.train_test_split(n_samples, test_size=500, random_state=k)
            splitter.initialize_with_random(batch_size, at_least_one_of_each_class=y[splitter.train], random_state=k)

            accuracies = []

            # The classic active learning loop
            for j in range(n_iter):
                model.fit(X[splitter.selected], y[splitter.selected])

                # Record metrics
                accuracies.append(model.score(X[splitter.test], y[splitter.test]))

                t0 = time()
                sampler.fit(X[splitter.selected], y[splitter.selected])
                selected = sampler.select_samples(X[splitter.non_selected])
                splitter.add_batch(selected)

            all_accuracies.append(accuracies)

        x_data = np.arange(10, batch_size * (n_iter - 1) + 11, batch_size)
        plot_confidence_interval(x_data, all_accuracies, label='{} + {}'.format(starting_sampler_name, sampler_name))


plt.xlabel('Labeled samples')
plt.ylabel('Accuracy')
plt.legend()
plt.tight_layout()

plt.show()

Discussion

From this experiment on a subset of MNIST, we confirm the observation of the original work: Selecting the first batch of samples using a K-Means sampler increases the accuracy for the first few batches but does not improve the final result, at least on this dataset and with the query strategies we explore.

Estimated memory usage: 25 MB